EPJ B Highlight - Investigating the role of random walks in particle diffusion
- Details
- Published on 18 January 2024
Theoretical analysis reveals new insights into unusual patterns displayed by diffusing particles in recent experiments.
Several recent experiments identify unusual patterns in particle diffusion, hinting at some underlying complexity in the process which physicists have yet to discover. Through new analysis published in EPJ B, Adrian Pacheco-Pozo and Igor Sokolov at Humboldt University of Berlin show how this behaviour emerges through strong correlations between the positions of diffusing particles travelling along similar trajectories. Their results could help researchers to create better models of the diffusion process – ultimately drawing deeper insights into how fluids behave.
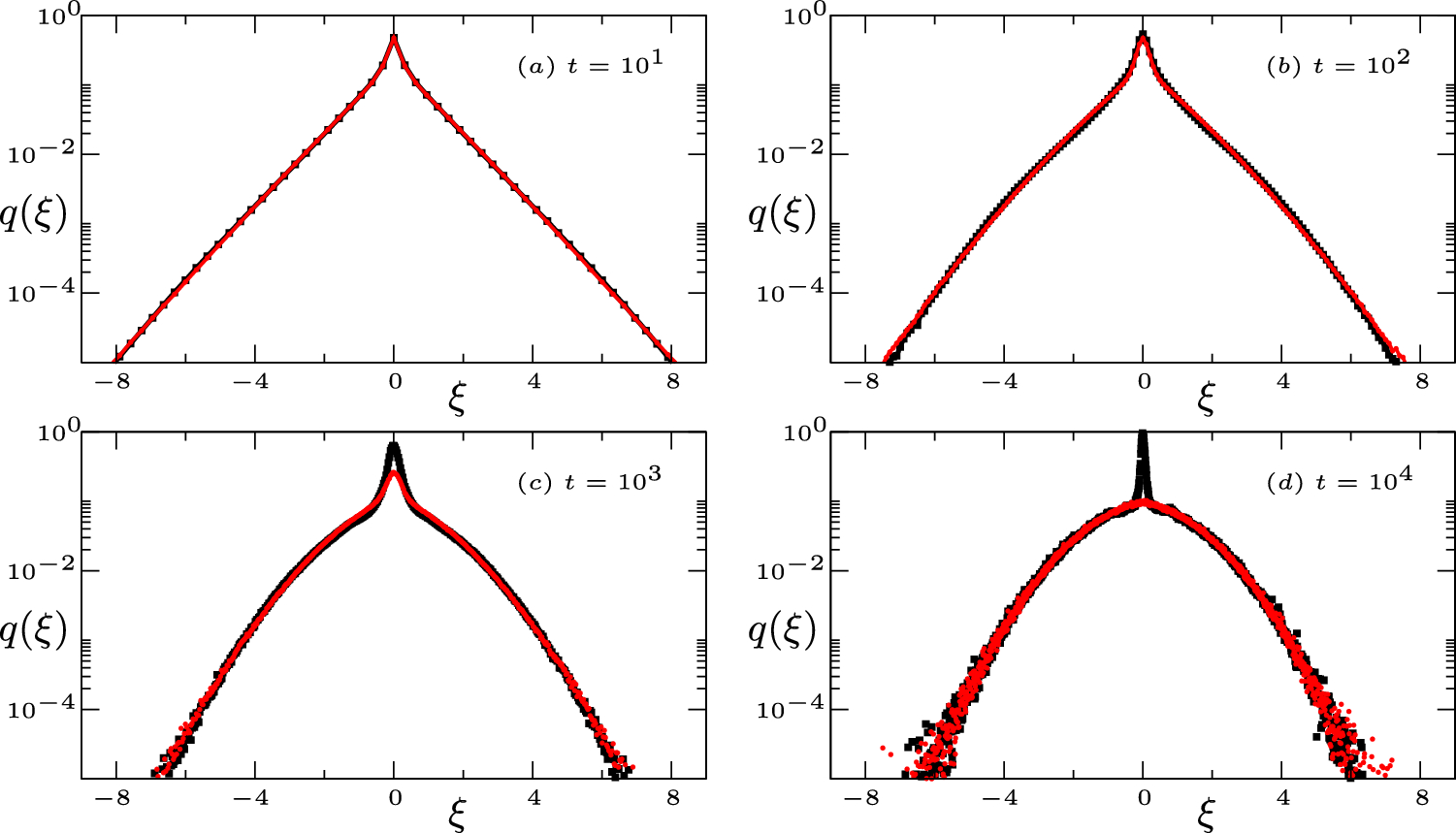
In many cases, diffusion occurs through random fluctuations in the positions of particles as they are jostled around by their neighbours. Known as Brownian motion, this effect can be visualised mathematically using normal distribution: a bell-shaped curve which illustrates the probability of finding a particle at any given displacement from its starting position. Yet in some situations, this distribution can feature a sharp peak at its centre – the very top of the bell curve – where the likelihood of finding particles is especially high. This behaviour has much in common with theoretical models characterised by diffusion rates which vary between localised regions – where in contrast to the expectation that the central peak will smooth out over time, it actually narrows and remains sharp.
In their study, Pacheco-Pozo and Sokolov investigated the nature of this persistent peak by considering the mathematics of ‘continuous-time random walk’ models. Here, a diffusing particle waits for a random amount of time before jumping to a new position – and the longer it waits, the further it jumps. In this case, the duo showed that a sharp central peak emerges through strong correlations between the displacements of jumping particles following similar trajectories, both in time and space. All the same, the continuous-time random walk model couldn’t fully match the shape of the sharp peak. This suggests the importance of more complex time-varying connections between particles, which the researchers now hope to investigate in their future studies.
Pacheco-Pozo, A., Sokolov, I.M. Random walks in correlated diffusivity landscapes. Eur. Phys. J. B 96:152 (2023). https://doi.org/10.1140/epjb/s10051-023-00621-z
Topical Collections
Open calls for papers
-
EPJ AM Call for papers: Themed Issue on Global Advances in Electromagnetic Metasurfaces for Space
(EPJ AM)
-
Call for papers : Special Issue on Imaging, Diffraction, and Spectroscopy on the micro/nanoscale
(EPJ AP)
-
EPJ C Topical Collection on String theory predictions for astroparticle and collider physics, and beyond
(EPJ C)

