About EPJ
The European Physical Journal (EPJ) is a series of peer-reviewed journals covering the whole spectrum of physics and related interdisciplinary subjects. EPJ is committed to high scientific quality in publishing and is indexed in all main citation databases.
Latest news
EPJ H Highlight - Lev Strum: A forgotten physicist who predicted the foundations of tachyon theory
- Details
- Published on 27 June 2025

A new paper reviews the life and career of Lev Strum: a little-known physicist who faced a tragic fate, and whose ideas about faster-than-light travel were revived decades later with the emergence of tachyon theory.
Ever since Einstein developed his theory of Special Relativity in 1905, physicists have widely accepted that no particle or information-carrying signal can ever travel faster than the speed of light in a vacuum. Following Einstein’s theory, however, the idea persisted that faster-than-light motions could still be possible in some cases. By far the most well-known revival of this idea was the emergence of tachyon theory in the 1960s.
Decades earlier, however, many of the most important elements of tachyon theory were also proposed by Lev Strum: a Ukrainian-Jewish physicist who ultimately faced a tragic fate, and whose name has been almost entirely forgotten. Through a new study published in EPJ H: Historical Perspectives on Contemporary Physics, Helge Kragh at the University of Copenhagen reviews the ideas proposed by Strum, and presents a biography of his life and scientific career.
EPJ D Highlight - Bound and virtual states in low-energy electron and positron scattering
- Details
- Published on 27 June 2025
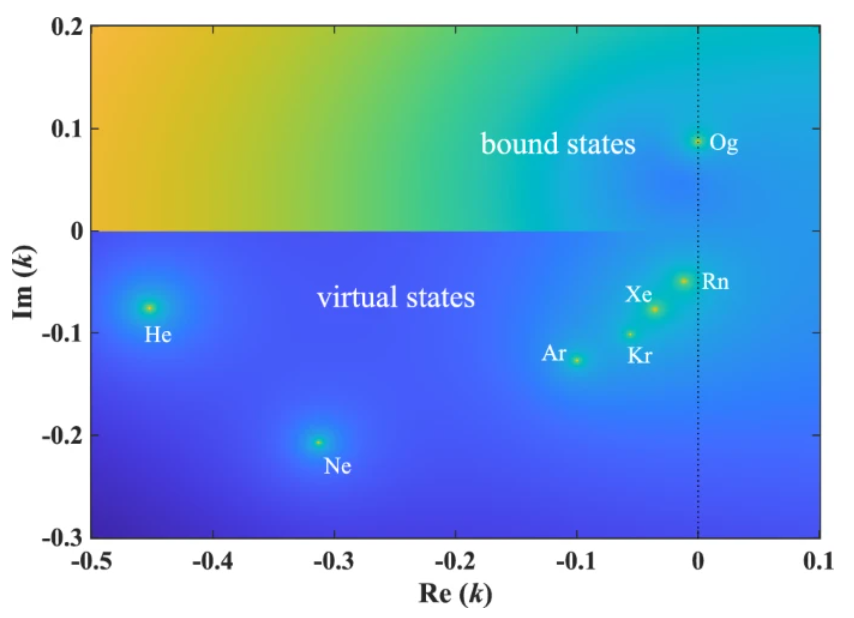
New mathematical approach confirms that low-energy charged particles can briefly bind to atoms or molecules
So far, it has remained an open question whether moving charged particles can briefly form bound states with neutral atoms and molecules. In previous experiments, researchers observed enhanced positron annihilation at energies corresponding to specific vibrational modes in neutral molecules, which they interpreted as evidence that the positrons were briefly bound. Until now, however, this interpretation has not yet been corroborated through other scattering observables.
Through new research published in EPJ D, Kamil Fedus and Grzegorz Karwasz at Nicolaus Copernicus University, Poland, present a new method for estimating the energies of both bound and virtual states of low-energy charged particles from elastic scattering cross-sections. Their approach confirms previous theoretical predictions about the formation of bound and virtual states during the scattering of these particles—helping physicists better understand how the scattering process unfolds.
EPJ B Highlight - Predicting adsorption with quantum indicators
- Details
- Published on 27 June 2025
A new mathematical framework predicts how solid materials adsorb to surfaces, using five quantum-based indicators of their constituent atoms
Many areas of research are challenged by the need to explain the properties of materials based on the quantum behaviour of their atoms. One particularly difficult effect to describe is the adsorption of solid materials onto other solid surfaces. Currently, this is often approached using band-based models, which consider groups of electron energy level, or ‘bands’, in the atoms that make up a material. However, these models have limited accuracy, especially when trying to connect quantum details with practical outcomes.
In new research published in EPJ B, Yonghui Li and colleagues at Tianjin University, China, introduce a method that more accurately predicts how strongly atoms in a material will adsorb to other surfaces. Their approach is based on a set of five key indicators, offering a more complete picture of how adsorption is controlled by atomic electron bands. This could have wide-ranging applications in areas such as materials design, catalysis, and biological systems.
Topical Collections
Open calls for papers
-
EPJ AM Call for papers: Themed Issue on Global Advances in Electromagnetic Metasurfaces for Space
(EPJ AM)
-
Call for papers : Special Issue on Imaging, Diffraction, and Spectroscopy on the micro/nanoscale
(EPJ AP)
-
EPJ C Topical Collection on String theory predictions for astroparticle and collider physics, and beyond
(EPJ C)





